Ellipse, một đường cong thú vị !

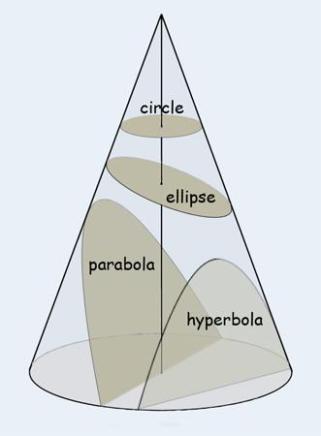
Khi nhắc đến hình ellipse, bạn sẽ nghĩ đến cái hình méo méo gần giống hình tròn. Trong toán học, hình ellipse được tạo thành khi cắt một hình nón bởi một mặt phẳng như hình dưới, hình giao bởi mặt phẳng cắt và hình nón chính là hình ellipse. Như vậy ta thấy rằng hình tròn cũng là một hình ellipse khi cắt hình nón bởi mặt phẳng song song với đáy hình nón.

Một điều thú vị nữa là nếu ta cắt hình nón bởi những mặt phẳng khác nhau, ta sẽ thu được các đường parabol hay hyperbol. Do vậy 3 đường ellipse, parabol, hyperbol nói chung gọi là các đường conic nhằm nói lên các đường này có liên quan đến hình nón (trong tiếng Anh, cone là hình nón)

Định nghĩa ở trên chỉ mang tính hình ảnh giúp chúng ta có thể phần nào hình dung được dáng vẻ của ellipse. Một định nghĩa khác giúp chúng ta có thể xây dựng các công thức toán học về ellipse đó là: Đường bao gồm tất cả những điểm có tổng khoảng cách đến 2 điểm cho trước là hằng số. Hai điểm cho trước này gọi là tiêu điểm của ellipse. Như vậy, ellipse được xem như một “hình tròn có hai tâm”, ta có thể vẽ ellipse bằng cách buộc một sợi dây vào giữa 2 cây đinh, di chuyển bút chì sao cho dây luôn căng và bút chì sẽ vạch ra một hình ellipse.

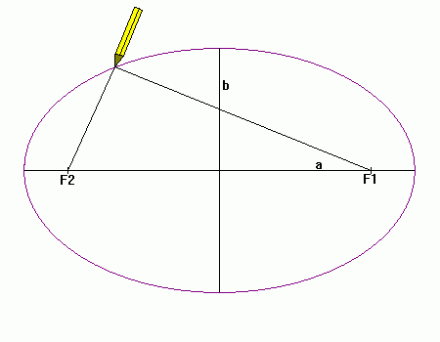
Từ định nghĩa trên ta có thể xây dựng phương trình của một ellipse trong hệ tọa độ Descartes. Xét một ellipse có các thông số như sau:

Ellipse và các thông số

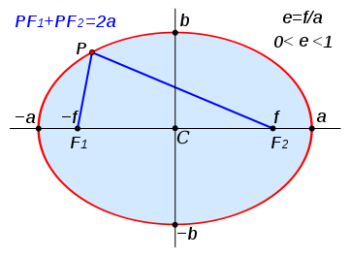
Bằng cách xét 1 điểm ở rìa ellipse và từ định nghĩa thu được . Gọi x,y là tọa độ của điểm P, do đó:

Chú ý rằng nếu cho P ở đỉnh ellipse (tọa độ b hoặc -b), ta thu được quan hệ giữa f và a,b:

Thay vào phương trình trên và rút gọn, ta được phương trình ellipse quen thuộc như sau:

Một cách biểu diễn ellipse khác ít được biết đến như cũng không kém phần thú vị đó là xem nó như một trường hợp đặc biệt của các Hypotrochoid. Một hình Hypotrochoid được định nghĩa là quỹ đạo vạch ra bởi 1 điểm trên một mâm xe khi mâm xe này lăn không trượt bên trong một khung tròn lớn:

Một quỹ đạo Hypotrochoid điển hình

Phương trình tham số của một Hypotrochoid được cho như sau:

Với R, r là bán kính của hình tròn lớn và bé, là góc hợp bởi trục Ox và đường nối tâm 2 đường tròn và d là độ dài đoạn thẳng nối tâm đường tròn bé với điểm vạch ra quỹ đạo.

Trong trường hợp R=2r, ta được:

Đây là phương trình của một ellipse có a=r+d và b=r-d. Do vậy quỹ đạo vạch ra có dạng một ellipse:

Trong trường hợp R=2r, quỹ đạo sẽ có dạng 1 ellipse

Bạn tính diện tích của hình ellipse bằng cách nào ? Thông thường để tìm diện tích của một hình ta thường áp dụng tích phân ydx, trong trường hợp ellipse ta phải tính tích phân sau:

Tích phân này không khó, nhưng nếu “tinh tế” hơn, ta có thể tìm diện tích của ellipse mà không cần phải tính tích phân. Bằng cách xét một hình tròn bán kính a có tâm trùng với tâm của ellipse, như vậy đường tròn này có phương trình:

Và ta cũng có thể đưa phương trình ellipse về dạng:

Bằng cách so sánh 2 phương trình trên, ta nhận xét rằng nếu 2 điểm trên ellipse và đường tròn có cùng hoành độ thì tung độ của chúng hơn nhau với tỷ lệ b/a. Do đó tỷ lệ diện tích của chúng cũng là b/a và do vậy diện tích của ellipse là:

Tính diện tích Ellipse thì dễ, thế còn chu vi của nó thì sao? Hãy cẩn thận! Đây là một vấn đề làm đau đầu các nhà toán học khi trong quá trình tính chu vi, ta phải tính tích phân:

Tích phân này không thể biểu diễn bởi các hàm cơ bản, nên nó trở thành một phần nghiên cứu riêng biệt trong tích phân, gọi là tích phân Eliptic vì nó liên quan đến bài toán tìm chu vi của Ellipse.

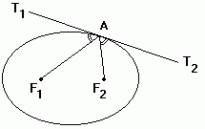
Một tính chất đặc biệt và quan trọng khác của ellipse, đó là tiếp tuyến của một điểm bất kỳ trên ellipse hợp với đường nối điểm đó với 2 tiêu điểm những góc bằng nhau.

Điều này có thể chứng minh bằng toán học, nhưng ở đây mình xin trình bày một cách chứng minh bằng Vật lý như sau: Giả sử ta có một cái khung cứng hình ellipse đặt cố định trên mặt bàn nằm ngang. Đục hai lỗ trên mặt bàn tại 2 tiêu điểm của khung hình ellipse. Tiếp đến luồn vào khung một hình vành khuyên sao cho vành khuyên có thể trượt không ma sát trên khung. Ta buộc hình vành khuyên bằng hai sợi dây không dãn và luồn hai đầu dây tương ứng qua 2 lỗ tiêu điểm, 2 đầu sợi dây được buộc vào 2 vật nặng có khối lượng bằng nhau. Ta thấy rằng thế năng của hai vật nặng tỷ lệ với độ dài sợi dây, nhưng khi dịch chuyển vành khuyên trên khung, tổng độ dài sợi dây là không đổi vì tính chất của hình ellipse, do đó thế năng của hệ là không đổi khi dịch chuyển khung trên sợi dây. Áp dụng nguyên lý thế năng cực tiểu, ta suy ra hình vành khuyên luôn cân bằng tại mọi vị trí trên khung, do đó hình chiếu của các lực căng dây lên tiếp tuyến là bằng nhau, và vì độ lớn lực căng là bằng nhau nên các góc là bằng nhau.

Tính chất này của ellipse cho ta một nhận xét là nếu ta có một bức tường hình ellipse, 2 cầu thủ đứng tại 2 tiêu điểm của ellipse, nếu một trong hai đá quả bóng thì cho dù không cần nhắm hay điều chỉnh hướng đá, quả bóng sẽ “bật tường” sẽ tìm đến đúng vị trí của cầu thủ kia, và nếu cầu thủ kia quyết định làm độc tác giả không chạm bóng, thì bóng sau khi bật tường sẽ lại tìm trở lại vị trí cầu thủ ban đầu. Quả là một tính chất khiến các cầu thủ Barcelona phải tôn làm sư phụ! Đây cũng là một ứng dụng khá phổ biến trong quang học và sóng cơ dùng để tập trung cường độ sóng tại một điểm.

Khoảng các từ tâm ellipse đến gốc tọa độ luôn không đổi

Một tính chất thú vị nữa của ellipse là nếu ta đặt một hình ellipse  vào một góc 1/4 nào đó sao cho nó tiếp xúc với 2 trục Ox và Oy, nếu ta xoay ellipse thì khoảng cách từ gốc tọa độ đến tâm ellipse luôn không đổi. Tính chất này xin dành các bạn chứng minh, bằng toán học hay vật lý tùy thích nhưng nếu bằng vật lý sẽ thú vị hơn !